Background

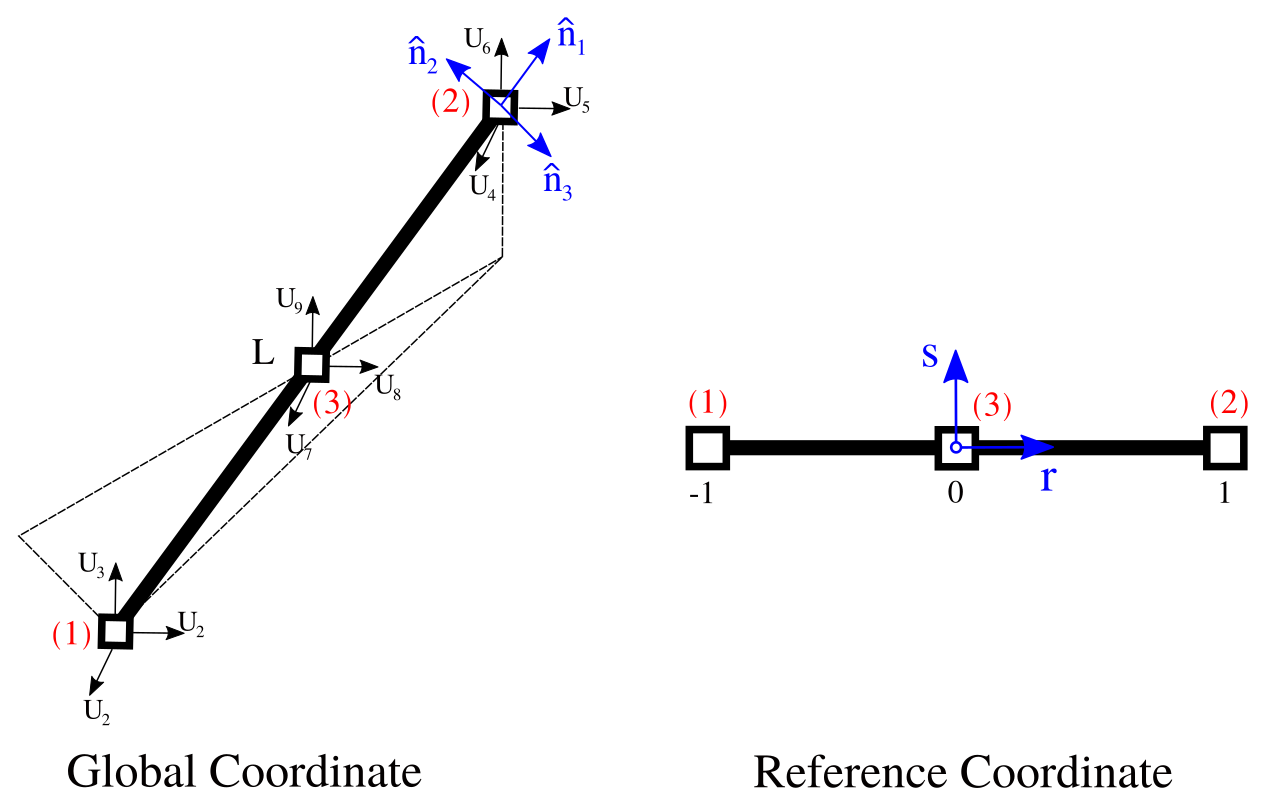
The lin3DTruss3 class creates a linearized three-dimensional truss element with three-nodes. Each node has three degrees-of-freedom, and each degree-of-freedom represents a translation in the X-, Y- and Z-directions. The Figure provides a simple representation of this element in which the local coordinates are represented by the r-axis, and (1), (2), and (3) represent the nodes of the element respectively. The element mass, damping and stiffness matrices, as well as internal force vector are computed in local-coordinate and then transformed into global coordinates. Numerical integration is performed to compute matrices and vectors.

The coordinates of any point \(x_1,x_2,x_3\) in the element is written in terms of the shape functions \(\textbf{N}_\textrm{i}(r)\) in the reference coordinates and the values of the i-th element nodal coordinates \(x^\textrm{(i)}_\textrm{j}\) as follows

\[ x_\textrm{j}^\textrm{e}(r ) = \sum_\textrm{i = 1}^{\textrm{N}_\textrm{n}} x^\textrm{(i)}_\textrm{j} \, \textbf{N}_\textrm{i}^\textrm{e}(r) \,. \]

The same transformation is used to evaluate the displacements within the element–i.e., \(u_\textrm{j}^\textrm{e}(r)\). Then, the displacement field is approximated as

\[ u_\textrm{j}^\textrm{e}(r) = \sum_\textrm{i = 1}^{\textrm{N}_\textrm{n}} u^\textrm{(i)}_\textrm{j} \, \textbf{N}_\textrm{i}^\textrm{e}(r) \,. \]

Since both the displacement field and the point element coordinates are approximated using the same shape function, this formulation is commonly known as isoparametric transformation.

Computation of the strain-displacement matrix \(\textbf{B}^\textrm{e}(x_1)\) now requires to be mapped into the reference coordinate systems. Application of the chain rule for differentiation to the shape functions yields

\[ \frac{\partial N_\textrm{i}}{\partial r} = \frac{\partial x}{\partial r} \frac{\partial N_\textrm{i}}{\partial x} = \mathbf{J} \frac{\partial N_\textrm{i}}{\partial x} \,, \]

where \(\mathbf{J}: \mathbb{R} \to \mathbb{R}\) is called the Jacobian matrix, here \(\mathbf{J} = \frac{L}{2}\). Hence, derivatives in \(\textbf{B}^\textrm{e}(x_1)\) can be transformed into \(\textbf{B}^\textrm{e}(r)\) in the reference coordinates using the Jacobian matrix.

The thre shape functions \(\textbf{N}_\textrm{i}^\textrm{e}(r)\) required to evaluate the shape function matrix \(\textbf{N}^\textrm{e}(r)\), the strain-displacement matrix \(\textbf{B}^\textrm{e}(r)\), and Jacobian matrix \(\textbf{J}^\textrm{e}(r)\) are:

\[ \textbf{N}_\textrm{1}^\textrm{e}(r ) = \frac{1}{2} r (1 - r) \,, \\ \textbf{N}_\textrm{2}^\textrm{e}(r ) = \frac{1}{2} r (1 + r) \,, \\ \textbf{N}_\textrm{3}^\textrm{e}(r ) = 1 - r^2 \,, \]

The isoparametric transformation has the advantage that every element is treated in the same manner. In this regard, mass and stiffness matrices as well as force vector are evaluated using the same reference coordinates as follows

\[ \mathcal{M}^\textrm{e} = \int_{-1}^1 {\textbf{N}^\textrm{e}} (r)^\top \, \rho^\textrm{e} \, \textbf{N}^\textrm{e}(r) \det \mathbf{J}^\textrm{e} \, dr \,, \\ \mathcal{K}^\textrm{e} = \int_{-1}^1 {\textbf{B}^\textrm{e}} (r)^\top \, \mathbb{C}^\textrm{e} \, \textbf{B}^\textrm{e}(r) \det \mathbf{J}^\textrm{e} \, dr \,, \\ \mathcal{F}^\textrm{e} = \int_{-1}^1 {\textbf{N}^\textrm{e}} (r)^\top \, \textbf{F}_b^\textrm{e} \det \mathbf{J}^\textrm{e} \, dr \,. \]

The mass and stiffness matrices as well as the force vector are transformed into global coordinates as \(\textbf{M}^\textrm{e} = \textbf{T}_\textrm{e}^\top \mathcal{M}^\textrm{e} \,\textbf{T}_\textrm{e}\), \(\textbf{K}^\textrm{e} = \textbf{T}_\textrm{e}^\top \mathcal{K}^\textrm{e} \,\textbf{T}_\textrm{e}\), and \(\textbf{F}^\textrm{e} = \textbf{T}_\textrm{e}^\top \mathcal{F}^\textrm{e}\). The transformation matrix from local to global axes is \(\textbf{T}_\textrm{e} = \begin{bmatrix} \hat{\textrm{n}}_1^\top & 0 & 0 \\ 0 & \hat{\textrm{n}}_1^\top & 0 \\ 0 & 0 & \hat{\textrm{n}}_1^\top \end{bmatrix}\), where \(\hat{\textrm{n}}_1 \in \mathbb{R}^{3}\) is the unit vector along the truss. Note that \(\textbf{M}^\textrm{e}, \textbf{C}^\textrm{e} , \textbf{K}^\textrm{e} \in \mathbb{R}^{\textrm{N}_\textrm{dof}^\textrm{e} \times \textrm{N}_\textrm{dof}^\textrm{e}}\) with \(\textrm{N}_\textrm{dof}^\textrm{e} = 9\) in this case.

REFERENCE:

Bathe, K. Jurgen, "Finite Element Procedures", Chapter 5: pages 339-340 (example 5.2: in 348-349). Prentice-Hall, 1996.

Pre-Analysis

The python Pre-Analysis in the 01-Pre_Process/Method/Attach.py file provides with an interface to populate the Entities dictionary. This file contains several functions to populate specific fields. For example, to create a lin3DTruss3, using json format, use:

addElement(tag, name='lin3DTruss3', conn, attributes):
- tag : The identifier of this element, i.e., tag > -1
- name : Seismo-VLAB element class name
- conn : Connectivity array of this element
- attributes : Specific properties for the created element, for example
  - 'material' is the hight of the line cross section.
  - 'area' is the cross section area.
  - 'rule' The integration rule to apply: GAUSS, LOBATTO.
  - 'np' Number of quadrature-points used for the integration.
Example

A LIN3DTRUSS3 element can be defined using the python interface as follows:
SVL.addElement(tag=1, name='lin3DTruss3', conn=[1,2,3], attributes={'area': 0.5, 'material': 1, 'rule': 'GAUSS', 'np': 3})

Application
Please refer to the C16-ST_Lin_3DSurface_Elastic_Truss3 file located at 03-Validations/01-Debugging/ to see an example on how to define a lin3DTruss3 element.

On the contrary, the 01-Pre_Process/Method/Remove.py file provides with an interface to depopulate the Entities dictionary. For example, to remove an already define Element, use:

delElement(tag):
- tag : The identifier of the element to be removed, i.e., tag > -1

Run-Analysis

The C++ Run-Analysis in the 02-Run_Process/04-Elements/03-Truss/lin3DTruss3.cpp file provides the class implementation. A lin3DTruss3 element is created using the built-in json parse-structure provided in the Driver.hpp. A lin3DTruss3 is defined inside the "Elements" json field indicating its "Tag" as follows,

{
    "Elements": {
        "Tag": {
            "name" : "LIN3DTRUSS3",
            "conn" : [ ],
            "attributes": {
                "np": int
                "rule": str
                "area": double,
                "material": int
            }
        }
    }
}

Variable	Description
`Tag`	Unique element object identifier.
`conn`	The element connectivity node array.
`area`	The cross-section area of the element.
`np`	Number of quadrature-points used for the integration.
`rule`	The quadrature integration name `rule`=GAUSS, LOBATTO.
`material`	The biaxial material identifier.

Attention: This formulation only allows small deformations.; Material non-linearity can be used in this element.; Currently the number of integration points np= 1,2,3,4,5,6,7 are supported, another value assumes np=3.; The material is considered to be the same at each quadrature point.; For the element size \(\Delta_\textrm{h}\) in wave propagation problems, one can consider about 12 points in one wavelength (this is 11 elements per wavelength) (the one with the maximum frequency). Once the mesh size is fixed, satisfying CFL condition to determine \(\Delta_\textrm{t}\) (i.e, \(\Delta_\textrm{t} \leq 0.9\,\Delta_\textrm{h}/V_p\), with \(V_p\) the p-wave velocity) for time marching is required.

Example

A LIN3DTRUSS3 element of area 0.01 with 3 integration points between nodes 1, 2, and 3, made of material 1 is constructed as:
{ "Elements": { "1": { "name" : "LIN3DTRUSS3", "conn" : [1,2,3], "attributes": { "np": 3 "rule": "GAUSS" "area": 0.01, "material": 1 } } } }